Apprenez À Rencontrer Le Point Sur La Droite Et Maîtrisez L’art De Le Déterminer Facilement. Suivez Nos Astuces Pour Trouver Ce Point Essentiel!
**comprendre Le Point Sur Une Droite**
- Qu’est-ce Qu’un Point Sur Une Droite?
- Les Coordonnées : Comprendre Les Abscisses Et Ordonnées
- La Représentation Graphique D’un Point Sur Un Plan
- Les Relations Entre Plusieurs Points Sur Une Droite
- L’importance Des Points Dans La Géométrie Analytique
- Applications Pratiques Des Points Sur Une Droite
Qu’est-ce Qu’un Point Sur Une Droite?
Un point sur une droite est une notion fondamentale en géométrie. Il représente une position précise sur cette droite, exprimée par un ensemble de coordonnées. Chaque point a sa propre identité et est souvent utilisé pour illustrer des concepts mathématiques complexes. Dans la vie quotidienne, nous pouvons penser à un point sur une droite comme une petite balise indiquant un emplacement spécifique, semblable à un médicament que l’on “Prescrit” pour un besoin médical.
Les coordonnées d’un point, formées par des abscisses et des ordonnées, nous permettent de situer ce point sur un plan. Imaginez une pharmacie où chaque médicament a sa place: les “Happy Pills” dans un coin, et les “Generics” dans un autre. De même, un point sur une droite se trouve grâce à ces coordonnées, qui agissent comme une carte permettant de naviguer dans l’environnement mathématique.
La représentation graphique d’un point augmente notre compréhension. Sur un graphique, un point se dessine comme une petite intersection, tout comme un “Count and Pour” de médicaments dans un flacon. Cela nous aide à visualiser les relations entre différents points sur une même droite, renforçant notre capacité à effectuer des analyses.
Pour conclure, l’importance de ces points dépasse la géométrie. Ils jouent un rôle crucial dans la géométrie analytique, un domaine qui s’étudie à travers des relations et des transformations. Chaque point sur une droite contribue à une compréhension plus large, tout comme chaque médicament, bien qu’uniquement “On the Counter” ou en prescription, a un impact dans notre vie quotidienne.
| Point | Coordonnées |
|---|---|
| A | (2, 3) |
| B | (4, 5) |
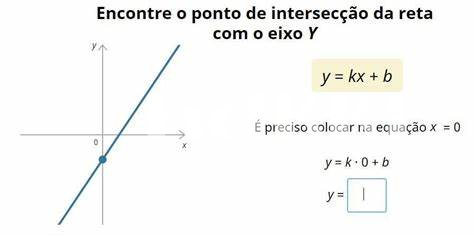
Les Coordonnées : Comprendre Les Abscisses Et Ordonnées
Lorsque l’on parle des coordonnées d’un point, il est essentiel de souligner la distinction entre abscisses et ordonnées. L’abscisse représente la position horizontale d’un point sur un système de coordonnées, tandis que l’ordonnée indique sa position verticale. Par exemple, si vous envisagez de localiser un point sur une droite, il est crucial de définir ces deux valeurs avec précision. Imaginez que vous devez prescrire des médicaments : si l’auteur de l’ordonnance note mal l’abscisse de la “happy pill” que vous devez donner à un patient, cela peut entraîner des conséquences indésirables. Ainsi, une compréhension claire de ces coordonnées nous permet de mieux naviguer dans les graphiques et de localiser précisément les points.
Ces concepts ne sont pas seulement théoriques. En pratique, l’interaction entre les abscisses et les ordonnées peut être comparée à la façon dont un pharmacien doit jongler avec divers ordres et prescriptions. Lorsqu’un patient vient chercher son traitement, le pharmacien doit rapidement “count and pour” les médications nécessaires, se familiarisant avec les valeurs correctes pour éviter des erreurs. Afin de realmente encontre o ponto sobre a reta, il est impératif que chaque élément soit en harmonie. La précision des coordonnées aide non seulement à résoudre des problèmes géométriques mais aussi à garantir que les médicaments sont administrés de manière appropriée, tout comme une bonne ordonnance assure une guérison rapide.

La Représentation Graphique D’un Point Sur Un Plan
Dans le cadre de la géométrie analytique, la représentation visuelle joue un rôle fondamental. Lorsque nous voulons comprendre comment se positionner un point sur un plan, il convient d’observer comment ce dernier se retrouve inscrit dans un système de coordonnées. Chaque point est défini par ses abscisses et ordonnées, ce qui nous permet de situer avec précision “encontre o ponto sobre a reta”. Imaginez un tableau croisé : les lignes verticales et horizontales se rejoignent pour former un canevas où chaque intersection correspond à un point unique.
En se penchant sur un point spécifique, tel qu’un médicament sur l’étagère d’une pharmacie, il est essentiel de percevoir la manière dont il s’intègre dans l’ensemble. Prenons, par exemple, l’idée d’une “Pharm Party”. Chaque point sur le plan peut être vu comme un participant à cette fête où les échanges et les interactions contribuent à un tableau dynamique. Ainsi, la représentation graphique d’un point sur un plan ne se limite pas à son existence isolée, mais se connecte à un réseau de relations, tout comme des amis se réunissant autour du même objectif.
La clarté est primordiale dans la représentation d’un point. En employant des couleurs distinctes et des étiquettes claires, on s’assure que chacun puisse identifier facilement le message véhiculé. Cela rappelle la nécessité d’une prescription bien rédigée, où chaque détail a son importance. L’utilisation de Tall Man Lettering pour différencier les médicaments devrait être la norme tout comme la précision d’un positionnement sur un graphique.
À mesure que l’on explore davantage, on découvre que chaque point peut également affecter les autres de manière significative. Les interactions possibles évoquent la gestion des prescriptions, où chaque décision prise peut avoir des répercussions sur la santé collective. Ainsi, il devient indispensable de visualiser ces relations non seulement pour comprendre l’importance de chaque point, mais aussi pour anticiper les résultats qui en découleront.

Les Relations Entre Plusieurs Points Sur Une Droite
Dans le cadre de la géométrie analytique, la position de plusieurs points sur une droite révèle des relations fascinantes et essentielles. Chaque point peut être décrit par ses coordonnées, qui permettent de déterminer son positionnement relatif. En analysant les distances entre ces points, nous sommes en mesure de comprendre la structure de la droite elle-même, comme une ordonnance prescrite sur une série de traitements. Les relations d’alignement ou de colinéarité des points se manifestent souvent grâce à des systèmes d’équations, où résoudre pour une variable peut montrer comment ces points interagissent.
L’interaction entre plusieurs points peut également }ouvoir des applications pratiques dans divers domaines, de l’ingénierie à l’économie. Par exemple, dans une pharmacie, il pourrait être avantageux de comparer la position de différentes prescriptions sur un graphique afin de déterminer lesquelles doivent être remplies en priorité. De même, l’idée d’« encounter o ponto sobre a reta » capte l’attention sur la manière dont différents points se rassemblent pour créer une image complète, un aspect crucial lors de l’importance d’un diagnostic médical, où chaque détail compte. Une analyse minutieuse peut même prévenir une situation de “pharmageddon”, où une surconsommation de médicaments pourrait résulter d’une négligence.
En définitive, ces relations ne se limitent pas seulement à une représentation mathématique mais sont aussi cruciales pour des décisions stratégiques dans des contextes variés. Comprendre comment et pourquoi les points s’articulent autour d’une droite permet d’atteindre des objectifs plus larges, qu’il s’agisse de garantir une gestion efficace des prescriptions ou d’optimiser les ressources dans n’importe quel système. C’est au travers de ces connexions que nous pouvons réellement saisir les implications de chaque point, transformant ainsi la simple géométrie en un outil puissant pour la résolution de problèmes complexes.

L’importance Des Points Dans La Géométrie Analytique
Dans le monde fascinant de la géométrie analytique, chaque point sur une droite se transforme en un véritable acteur. Ces points, loin d’être de simples coordonnées, permettent de décrypter des informations essentielles sur la nature des lignes et des formes. En rencontrant un point sur une droite, on découvre non seulement sa position, mais aussi la relation qu’il entretient avec d’autres points. Ainsi, ces emplacements deviennent des pivots autour desquels s’articulent toutes sortes de calculs et d’analyses géométriques.
La signification des points dépasse le cadre théorique. Ils servent de référent, offrant une base solide pour la création de systèmes complexes. Les astronomes, par exemple, peuvent utiliser des points sur une droite pour modéliser les trajectoires des étoiles. En médecine, le traçage précis et la localisation de points peuvent s’avérer cruciaux pour des interventions chirurgicales. En d’autres termes, ces coordonnées sont comme des “happy pills” pour les mathématiciens, garantissant une clarté et une précision qui facilitent l’interprétation des données.
L’interconnexion entre les différents points crée des opportunités d’apprentissage et des découvertes. Grâce à une étude attentive des relations entre eux, il est possible d’établir des connexions et de développer des modèles prédictifs robustes. Cela encourage l’innovation, tant dans le domaine des sciences naturelles que des sciences appliquées, faisant de chaque point une pièce du puzzle. Les applications de ces concepts sont infinies, qu’il s’agisse de technologie, d’architecture ou même d’art. Voici un aperçu des divers domaines où les points jouent un rôle prépondérant :
| Domaine | Description |
|---|---|
| Astronomie | Modélisation des trajectoires des étoiles |
| Médecine | Localisation pour interventions chirurgicales |
| Technologie | Applications en data science et machine learning |
| Architecture | Création de designs et de structures solides |
| Art | Utilisation de points pour créer des motifs et compositions |
Applications Pratiques Des Points Sur Une Droite
Les points sur une droite ne se limitent pas à un simple exercice théorique ; ils ont des applications pratiques qui influencent divers aspects de la vie quotidienne, notamment dans le domaine de la santé. Prenons l’exemple du secteur pharmaceutique, où les prescriptions, souvent considérées comme des élixirs de bien-être, sont placées dans un contexte géométrique. Chaque point peut représenter un ensemble distinct de données d’un patient, comme le dosage de médicaments. Cela permet aux pharmaciens de mieux comprendre les besoins individuels des patients et de fournir des recommandations adaptées.
En médecine, la compréhension des relations entre plusieurs points s’avère cruciale pour la gestion des médicaments. Par exemple, le suivi des patients qui prennent des “happy pills” et leurs effets secondaires peut être modélisé à l’aide de coordonnées, permettant aux professionnels de la santé de visualiser les tendances au fil du temps. Cela est particulièrement important à une époque où les prescriptions peuvent changer rapidement et où il est nécessaire d’évaluer les interactions entre différents médicaments, appelés ici “cocktails”.
La capacité à cartographier ces points sur une droite aide également à la gestion de la pharmacie là où des événements comme le “Pharmageddon” peuvent survenir. Pendant ces périodes de forte affluence, il est vital de triager les prescriptions afin de garantir que les patients reçoivent leurs médicaments en temps et en heure. Les pharmaciens doivent donc être en mesure d’analyser rapidement les informations pour effectuer des thèmes de “Count and Pour”, optimisant ainsi le service après s’être assuré que les données sont correctement saisies.
Enfin, l’application de la géométrie analytique dans le domaine pharmaceutique facilite également les audits de prescription et les revues d’utilisation des médicaments (DUR). L’évaluation des points sur une droite permet une vue d’ensemble des schémas de prescription, aidant ainsi à détecter les abus tels que ceux observés dans les “pill mills”. En comprenant où ces abus se produisent, les autorités peuvent mieux réguler la distribution des substances contrôlées, garantissant ainsi la sécurité et l’efficacité du traitement médicamenteux pour tous.